
퍼셉트론에서 보았던 위 식을 다음과 같이 표현할 수 있다.
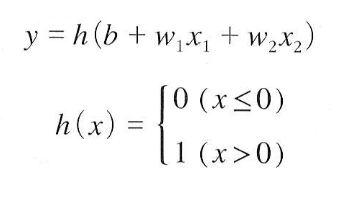
여기서 쓰인 h(x) 를 activation function (활성화 함수) 라고 부른다.
위 식은 step fucntion (계단 함수) 하고 하며
정리하면
"퍼셉트론에서는 활성화 함수로 계산함수를 이용한다" 가 된다.

활성화 함수는
step func, ReLU, sigmoid, softmax, tanh 등 여러가지가 있으며 nonlinear 하다는 특징이 있다.
sigmoid 함수


x가 커지면 h(x) = 1
작아지면 h(x) = 0
hidden layer 에서는 activation function 으로 ReLU 를 주로 사용한다.
아웃풋의 종류가 classification (분류) 인 경우 마지막에
- 두가지만 나누는 binary 의 경우 주로 sigmod 사용. ex) 고양이인지 강아지인지
- 3개 이상으로 나누는 multi calss 에서는 soft max 사용 ex) 고양이인지 강아지인지 사람인지
ReLU 함수
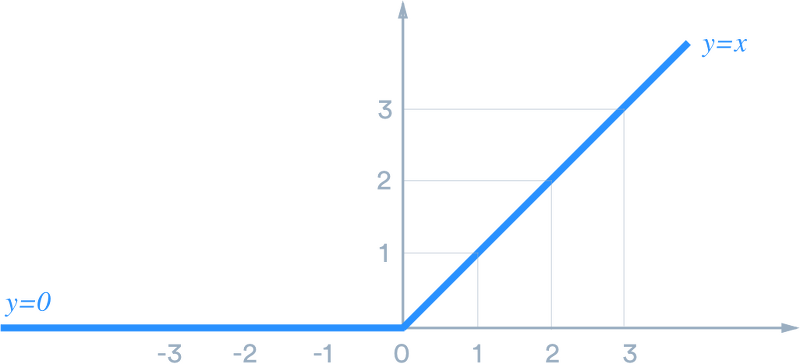


0 과 x 중 큰 값
아웃풋의 종류가 Regression(회귀) 일 경우
마지막에 Identity Function(항등함수)를 사용한다.
y(x) = x

행렬과 벡터의 곱으로 표현
벡터 x = [x1, x2] y = [y1, y2, y3] b = [b1, b2, b3]
W 는 행렬
y = Wx + b

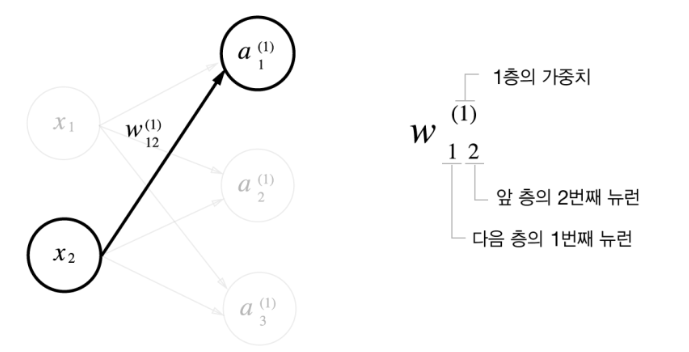
표기법
Optimization algorithm(최적화 알고리즘)
- Gradient Descent(경사하강법)

W, b -> Wopt, bopt (optimize)
위의 네트워크가 빨간색 함수로 동작하게끔 W 와 b 를 최적화한다.
최초의 값을 Winit, binit 이라고 하며 임의의 값을 넣는다.
binit은 보통 0벡터를 쓰고 행렬Winit은 가우시안 분포로 랜덤값을 준다.
랜덤값인 Winit, binit 에서 최적값인 Wopt, bopt 를 구하는 방법은 점직으로 조금씩 변화시키는 것이다.
ex)
x = 1 일 때, y = 3.45 가 정상값이라고 하자.
이 때 w1 = 0.53 로 해서 x = 1을 네트워크에 통과시켰더니 y = 1.5 라는 다른 값이 나왔다.
여기서 LOSS 를 구할 수 있는데 정상값과 결과값을 차의 제곱으로 표현한다.
LOSS = (1.5 - 3.45)^2 Squared Error 라고도 한다.
우리의 목표는 LOSS를 0으로 만드는 것이다.
위와 마찬가지로
x = 2 일 때, y = 5.67 이 정상값인데 결과값은 0.3이 나왔다고 하자.이때의 LOSS = Mean Squared Error = ((1.5 - 3.45)^2 + (0.3 - 5.67)^2) / 2 라고 한다.
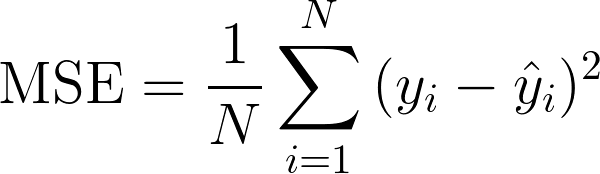

W1 = 0.53, y = 1.5 -> W1 = 0.54, y = 1.7 -> W1 = 0.55, y = 1.59 -> . . . -> W1 = 1.23, y = 3.45
위처럼 y 가 정상값이 나오게 하기 위해 w1 = 0.53 을 수정해야 한다. 그 방법은 LOSS를 W1에 대하여 편미분 하는 것이다. ∂(라운드) : 편미분 기호
∂LOSS / ∂W1

편미분을 통한 W1 최적화 방법은 아래와 같다.
∂LOSS / ∂W1 > 0 : W1을 증가시키면 LOSS가 증가한다는 뜻 -> W1 감소시킴
∂LOSS / ∂W1 < 0 : W1이 증가시키면 LOSS가 감소한다는 뜻 -> W1 증가시킴
위와 같은 최적화 알고리즘을 Gradient Descent(경사하강법) 이라고 한다.

learning rate 에타는 보통 0.01 이나 0.001 같은 아주 작은 값을 넣는다.
하지만 초기에는 빠르게 최적값에 접근하기 위해 조금 큰 값을 설정하고
최적값에 가까워지만 작은 값을 넣어서 세밀하게 접근하여 최적값에 도달한다.
이렇게 learning rate 를 조정하는 것을 gear shifting 이라고 한다.
최적값을 찾는 과정을 traning 이라고 하고
최적값 설정 후 새로운 값을 넣어서 정상 값이 나오는지 확인 하는 과정을 test 라고 한다.
Gradient vanishing (기울기 소실)
- hidden layer 로 sigmoid function 을 사용할 경우에 발생한다.


LOSS 를 Chain Rule에 의해 풀어서 표현하면 위의 식과 같다.
sigmoid function의 미분값의 범위는 (0, 0.25] 인데 이것을 계속 곱하면 w1값은 점점 작아져 0에 가까워진다.
이것을 gradient vanishing 이라고 한다.
그래서 hidden layer 에서의 activation function 은 보통 ReLU를 사용한다.
Backpropagation(역전파)
- W 와 b 를 설정하고 LOSS를 확안한 다음 다시 역으로 돌아다 네트워크를 업데이트하는 과정.
- Training 과정.
Forward-propagation(순전파)
- 인풋을 넣고 아웃풋을 확인. 다시 다른 인풋을 넣고 아웃풋을 확인.
- Test 과정.
Softmax function
- 출력으로 0~1사이의 값으로 모두 정규화하며 출력 값들의 총합은 항상 1이 되는 특성을 가진 함수이다.
- 출력 y는 0~1.0 사이의 실수이다.
- 출력을 '확률'로 해석할 수 있다.
- 출력의 총합은 1이다.




= 고양이일 확률
= 강아지일 확률
= 햄스터일 확률
주의해야 할 사항은 네트워크의 출력값이 e^x 와 같은 지수 형태라는 것이다.
e^x 가 너무 큰 값이 되면 overflow가 생겨 컴퓨터가 인식을 못해서 infinite 처리를 해버린다.

위 수식을 보면 softmax 의 지수 함수를 계산할 때 어떤 정수(C')를 더하거나 빼도 결과는 같음을 알 수 있다.
일반적으로 최댓값을 빼주고 softmax 함수를 통과시킨다.
multi class classification 에서는 LOSS 함수로 Cross Entropy Error 를 사용하는데
이 CEE를 계산하기 위해서는 확률적인 값이 필요해서 softmax를 쓰는 것이다.
LOSS 함수는 Training 과정에서 필요한 것이기 때문에
Test 과정에서는 원소의 대소 관계는 변하지 않는다는 특성으로 softmax 함수를 생략하는 것이 일반적이다.
MNIST 데이터셋
- 28 * 28 = 784개의 픽셀을 가지고 있고 0 ~ 9 사이의 숫자 이미지와 레이블로 구성된 데이터 셋
-> 입력 784개, 출력 10개

흑백사진은 각 픽셀의 값이 0(검) ~ 255(흰) 이어서, 255로 나눠서 0 ~ 1.0 사이의 값으로 normalize(정규화)함
normalize를 하는 이유는 뉴럴 네트워크가 인풋으로 가장 선호하는 값의 범위가 [-1, 1] 이기 때문이다.
pre-processing(전처리)
normalize 를 포괄하는 개념으로 뉴럴 네트워크에 편리하도록 인풋값에 특정한 변화를 주는 것을 말한다.
실제 현업에서는 전처리과정이 중요하다.
Batch 처리
- 1000개의 인풋이 있다면 n개씩 묶은 것(ex. 10개씩)
- 이미지 1장당 처리 시간을 대폭 줄여준다.
- 배치를 사용하는 이유 1 : 수치 계산 라이브러리 대부분이 큰 배열을 효율적으로 처리할 수 있도록 최적화되어 있다.
- 배치를 사용하는 이유 2 : 사이즈가 큰 뉴럴 네트워크는 병목현상이 발생하는데 배치 처리를 함으로써 부하를 줄인다.
사진 출처
https://gggggeun.tistory.com/121
https://brunch.co.kr/@chris-song/39
https://kingnamji.tistory.com/16
'딥러닝' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝 Chapter6 - 가중치의 초깃값 (0) | 2022.06.26 |
|---|---|
| 밑바닥부터 시작하는 딥러닝 Chapter6 - 학습 관련 기술들 (0) | 2022.06.26 |
| 밑바닥부터 시작하는 딥러닝 Chapter5 - 오차역전파법 (0) | 2022.06.25 |
| 밑바닥부터 시작하는 딥러닝 Chapter4 - 신경망 학습 (0) | 2022.06.17 |
| 밑바닥부터 시작하는 딥러닝 Chapter2 - Perceptron(퍼셉트론) (0) | 2022.06.13 |




댓글