[DB] 인덱스에서 B tree 를 쓰는 이유

 

 

 

 

 

B tree는 BST(Binary Search Tree, 이진 탐색 트리) 보다 확장된 형태입니다.

 

 

BST는 자식노드가 최대 2개인 트리
왼쪽 서브트리는 부모보다 작은 값, 오른쪽 서브트리는 부모보다 큰 값

B Tree는 이보다 확장되어 자식노드를 2개 이상 가질 수 있는 트리입니다.
모든 leaf 노드(최하위 노드)들은 같은 레벨에 있습니다.

최대 자식노드 수 M이 5 일 때 5차 B tree 라고 합니다.

 

최대 자식 수    M

최대 키 수       M-1

최소 자식 수    M/2의 올림        (root, leaf node 제외)

최소 키 수       M/2의 올림 – 1   (root node 제외)

 

 

 

 

DB 인덱스에 B tree 계열을 사용하는 이유

 

B tree 계열 (B+ tree, B* tree) 의 시간복잡도는 O(logN) 입니다.

마찬가지로 self balancing 하는 BST인 AVL tree와 Red-Black tree 도 O(logN) 입니다.

 

❓ 그런데 왜 B tree 계열을 사용할까요?

 

결론부터 말하자면

디스크 접근 횟수가 더 적고 (깊이)

적은 횟수로 데이터를 찾을 수 있고 (자식노드 수)

관련된 데이터를 한번에 많이 가져올 수 있기 때문입니다. (노드의 데이터 수)

 

 

위와 같은 결론이 나온 이유를 알기 위해 컴퓨터 구조를 살짝 보겠습니다.

 

컴퓨터는 다음과 같이 CPU - 메인메모리(RAM) - 디스크 순으로 실행됩니다.

 

 

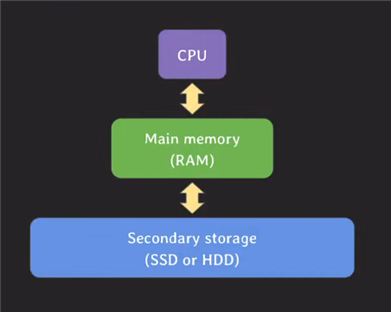
여기서 가장 아래에 있는 디스크의 특징을 보면

 

 

핵심 데이터 몇 개는 메인 메모리에 미리 올려놓고 나머지는 디스크에 있다가 select 같은 데이터 조회 요청이 오면 디스크에서 block 단위로 메모리에 올립니다.

 

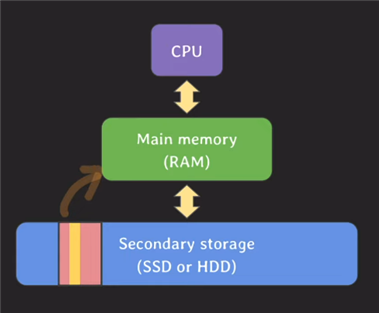
그래서 성능면에서는 디스크 접근횟수를 최대한 적게,

한 번 접근해서 block 단위로 가져올 때 관련 데이터를 더 많이

가져오는 것이 최적이 됩니다.

 

 

 

 

 

그러면 이제 아래 테이블의 b에 대해 B tree index(b) 와 AVL tree index(b) 를 생성했다고 보겠습니다.

 

 

현재 어떤 노드도 메모리에 올라가 있지 않은 상태라고 했을 때, 루트 노드(가 있는 block)부터 디스크에 접근해서 찾아 메모리로 가져옵니다. 이 과정에서 노드의 깊이, 디스크 접근 횟수, 자식노드 수, key 수 의 차이로 인해 성능 차이가 생깁니다.

 

그래서 B tree와 BST의 시간복잡도가 O(logN) 으로 같지만 위와 같은 차이로 인해 성능면에서 B tree가 더 좋기때문에 DB 인덱스에 사용하게 된 것입니다.

 

 

 

 

 

 

참고

 

https://www.youtube.com/watch?v=bqkcoSm_rCs&list=PLcXyemr8ZeoREWGhhZi5FZs6cvymjIBVe&index=26&t=5s&pp=iAQB

 

 

https://www.youtube.com/watch?v=H_u28u0usjA&list=PLcXyemr8ZeoREWGhhZi5FZs6cvymjIBVe&index=27&t=1943s&pp=iAQB

 

 

 

https://www.youtube.com/watch?v=liPSnc6Wzfk&list=PLcXyemr8ZeoREWGhhZi5FZs6cvymjIBVe&index=28&t=1308s&pp=iAQB